Hey friends! I assure you that this post would be one of the amazing posts by me. It was very fun to review my old notes and to go through some recent developments on this topic and I assure you to answer all your queries through this post.
Before initiating the topic, I would request you to throw away all the methodologies and mindsets for this topic and have a fresh start.
WHAT ARE VECTORS?:
In layman terms, a vector is a quantity that can be described with magnitude and direction. For example, a two-dimensional vector can be written as:
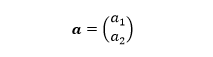
Similarly, a three and four-dimensional vector can be written as:

Therefore, the n-dimensional vector can be written as:
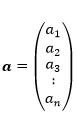
The a1,a2, a3, …, an are the parameters used to define a point with a position vector a, in n-dimensions.
WHAT IS 4-D SPACETIME?:
Albert Einstein visualized and mathematically formulated the universe as a 4-D spacetime. He thus used four parameters to define a position in spacetime, eg. (t, x, y, z) or
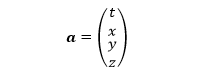
Einstein’s 4-D spacetime uses Minkowski’s structure rather less complex Euclidean 4-D space.
HOW DOES A FOUR-DIMENSIONAL OBJECT LOOKS LIKE?:
Higher-dimensional objects are much more complex to visualize than a three-dimensional object. This is since our neurotransmitters are aware of how a 3-D world looks like, however, unaware of how a 4-D world looks. The retina sees a two-dimensional image and our neurotransmitters convert them to the 3-D image.
Mathematics is the tool which can help us to ‘visualize’ how higher-dimensional objects would look like. A point is dimensionless and a one-dimensional line is comprised of two dimensionless points. Similarly, a two-dimensional square is comprised of four one-dimensional lines and a three-dimensional cube is comprised of six two-dimensional squares. Therefore, we can say by looking at the above trend that a four-dimensional hypercube (or tesseract) is comprised of eight three-dimensional cubes.
MORE ON TESSERACT:
Tesseract is a four-dimensional version of the 3-D cube, similarly as cube is a three-dimensional version of the 2-D square. As I said earlier, it’s difficult to visualize a higher dimensional object with our brain. Therefore, scientists use dimensional analogy to understand the nature of higher-dimensional space i.e. they study how (n-1) dimensions are related to n dimensions and then inferring how n dimensions would relate to (n+1) dimensions.
This analogy was used by Edwin Abbott (Shakespeare scholar) in his book ‘Flatland’. In his book, he narrated a story of a 2-D square living in a two-dimensional world. The square can move forward, backward, left and right, but cannot move up and down as it’s constrained to two-dimensions. On another hand, a 3-D cube is capable to move forward, backward, left, right, up and down. In the 2-D world, there is no conception of ‘height’ and their houses are absolutely flat. A 2-D object like square cannot see anything inside the house until and unless he goes inside. However, a 3-D object can easily see what’s inside the house from ‘up’ of the house. Therefore, from a perspective of the 2-D square, a three-dimensional being has seemingly God-like powers as it has the ability to remove or place objects without being visible by standing a few inches away in third-dimension.
Taking this concept to (n+1) dimension i.e. to four-dimensions. From our (3-D) perspective, a four-dimensional being would have God-like powers as it will have the ability to see everything that from a three-dimensional perspective is enclosed behind the walls.
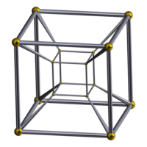
But how this four-dimensional being will look like? Another useful application of dimensional analogy is in projections i.e. projecting n-dimensional object in (n-1) dimensions and then inferring how (n+1) dimensional object would be projected in n dimensions. Take a 3-D cube and project its shadow on a 2-D surface. By dimensional analogy, we know that the 3-D cube will cast a shadow of two-dimensional squares joined by vertices. This is the same as we draw a cube on a piece of paper. As we lose dimension while casting a shadow of the cube, the authenticity of the cube’s geometry will be lost i.e. the lines will not be equal and perpendicular to adjacent lines.
Taking this analogy to (n+1) dimensions, a four-dimensional hypercube (tesseract) will cast a shadow of three-dimensional cubes joined by vertices. This projection is seen in the figure (NOTE: the visual presentation here is a two-dimensional image of the three-dimensional shadow of the four-dimensional hypercube (tesseract)).
WHAT’S THE SHAPE OF OUR UNIVERSE?:
Let’s see what is the universe and then see what its shape is? Universe is all of space and time and its contents, including all forms of matter and energy. In special theory of relativity, this spacetime is absolutely flat, however, in general theory of relativity, spacetime bends/curves in presence of matter or energy. In my last post, I talk about Einstein’s biggest blunder. However, in 1922, while Einstein and other physicists were looking for ways of avoiding general relativity’s nonstatic universe, Alexander Friedmann (Russian physicists and mathematician) instead, set about explaining it.
Friedmann made two assumptions, that, the universe is spatially homogenous and isotropic. With these assumptions, Friedmann showed, by solving the equations of general relativity, that, the universe is not static. Later in 1929, Hubble confirmed his then hypothesis.
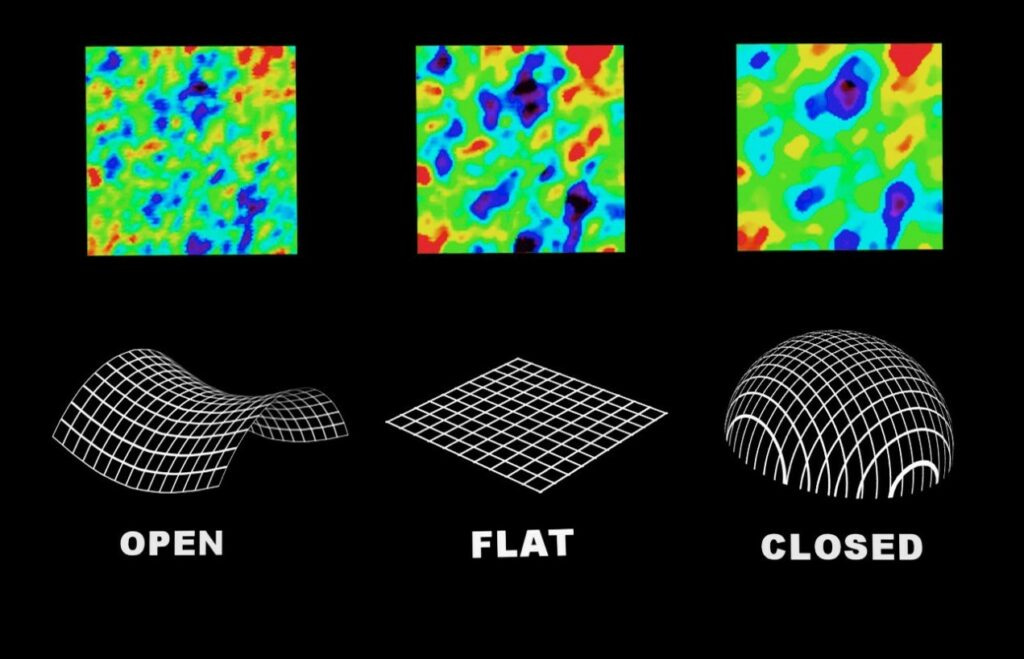
Friedmann derived only one model of the universe. But there are actually three possible types of solutions to Einstein’s equations i.e. three different kinds of Friedmann models or three different ways the universe can behave:
1. Flat Universe: The universe is expanding only just fast enough to avoid collapse. The speed at which the galaxies are moving apart gets smaller and smaller, but it never quite reaches zero. In this universe, space is absolutely flat and infinite. As the average density (amount of matter per unit volume) in this universe is exactly equal to the critical density, the universe will forever slow its expansion, ever more gradually approaching, but not ever reaching, a static size.
2. Closed Universe: The universe is expanding sufficiently slowly that the gravitational attraction between the different galaxies causes the expansion to slow down and eventually to stop. The galaxies then start to move toward each other, and the universe contracts. In this universe, space is positively curved, finite and it does not have any boundary. As the average density (amount of matter per unit volume) in this universe is greater than the critical density, the gravity is so strong that space is bent around onto itself i.e. into a four-dimensional hypersphere.
3. Open Universe: The universe is expanding so rapidly that the gravitational attraction can never stop it, though it does slow it down a bit. In this universe, space is negatively curved and infinite. As the average density (amount of matter per unit volume) in this universe is less than the critical density, there is not enough gravitational pull to stop the expansion, and the universe expands forever.
So what’s our shape of the universe? Which if the above Friedmann’s model fits? To answer this measuring the average density of our universe is necessary. If this energy density is less than the critical density, then, our universe will be negatively curved i.e. an open universe, if it’s more than the critical density, then, our universe will be positively curved i.e. a closed universe and if it’s less than the critical density, then, our universe will be negatively curved i.e. an open universe.
Present calculations and measurements turn out, that, the average density of our universe is equal to critical density with a 0.4% margin of error. In spite of considering the invisible 95.1% energy density of our universe (dark matter and dark energy) which I talked in the last post, our universe turns out to be flat and infinite.
REFERENCE BOOKS:







One response to “UNDERSTANDING THE FOURTH DIMENSION”
I am commenting to let you understand of the cool discovery my wife’s daughter enjoyed checking yuor web blog. She learned a lot of details, including what it’s like to have an incredible coaching heart to make the mediocre ones completely fully understand specified tortuous subject matter. You actually did more than our desires. Thank you for providing these precious, trusted, educational not to mention cool tips about your topic to Tanya.